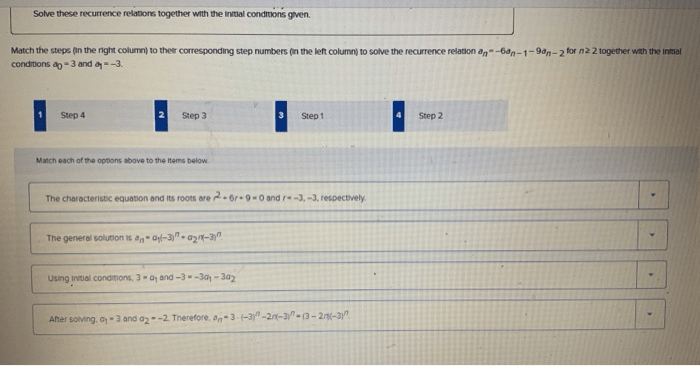
Solve these recurrence relations together with the initial conditions given – Delving into the realm of recurrence relations, this guide embarks on a journey to unravel the intricacies of these mathematical equations and their accompanying initial conditions. By shedding light on the diverse methods and techniques employed to solve them, we unlock their potential for modeling real-world phenomena and gaining insights into complex systems.
Recurrence relations, ubiquitous in fields ranging from computer science to biology, provide a powerful framework for representing and analyzing sequences of values that evolve over time. Understanding how to solve these relations, coupled with the appropriate initial conditions, empowers us to decipher the underlying patterns and predict future outcomes with remarkable precision.
Overview of Recurrence Relations

Recurrence relations are mathematical equations that define a sequence of terms, where each term is determined by the preceding terms. They play a crucial role in various fields, including computer science, mathematics, finance, and biology. Initial conditions are values that specify the starting point of a recurrence relation and are essential for solving it.
Common Methods for Solving Recurrence Relations
Method of Substitution
The method of substitution involves directly substituting the given recurrence relation into itself repeatedly until a closed-form solution is obtained. It is suitable for recurrence relations with a simple pattern.
Method of Generating Functions, Solve these recurrence relations together with the initial conditions given
The method of generating functions involves converting a recurrence relation into an equation involving a generating function, which is a formal power series whose coefficients encode the terms of the sequence. By manipulating the generating function, the closed-form solution can be derived.
Advanced Techniques for Solving Complex Recurrence Relations
Master Theorem
The Master Theorem is a powerful tool for analyzing the asymptotic behavior of recurrence relations of the form T(n) = aT(n/b) + f(n). It classifies recurrence relations into three types based on the values of a, b, and f(n), and provides a corresponding asymptotic bound.
Divide-and-Conquer Approach
The divide-and-conquer approach involves dividing the recurrence relation into smaller subproblems, solving the subproblems, and combining their solutions to obtain the solution to the original recurrence relation. This approach is particularly useful for recurrence relations with a divide-and-conquer structure.
Applications of Recurrence Relations in Real-World Scenarios
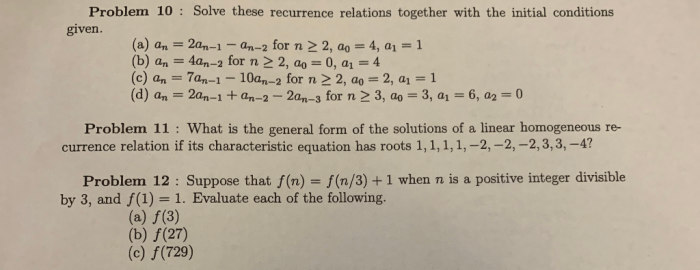
Computer Science
Recurrence relations are widely used in computer science to analyze the performance of algorithms, such as the running time and space complexity. They can be used to derive closed-form expressions for the number of operations or memory requirements of an algorithm.
Finance
Recurrence relations are employed in finance to model stock prices, interest rates, and other financial phenomena. By analyzing these recurrence relations, financial analysts can make predictions about future market trends and develop trading strategies.
Biology
In biology, recurrence relations are used to model population growth, disease spread, and other biological processes. They provide insights into the dynamics of these systems and help researchers understand their behavior over time.
Tips and Best Practices for Solving Recurrence Relations
To effectively solve recurrence relations, consider the following tips:
- Choose the appropriate method based on the structure of the recurrence relation.
- Consider boundary conditions and ensure that the initial conditions are satisfied.
- Organize your solution clearly, explaining the steps involved and providing justification for each step.
FAQ: Solve These Recurrence Relations Together With The Initial Conditions Given
What is the significance of initial conditions in solving recurrence relations?
Initial conditions play a crucial role in solving recurrence relations as they provide the starting values for the sequence. Without initial conditions, the recurrence relation cannot be uniquely determined, and multiple solutions may exist.
What are some common methods for solving recurrence relations?
Common methods for solving recurrence relations include the method of substitution, generating functions, the Master Theorem, and the divide-and-conquer approach.
How can recurrence relations be applied to real-world scenarios?
Recurrence relations have wide-ranging applications in computer science, finance, biology, and other fields. For instance, they are used to analyze algorithms, model stock prices, and simulate population growth.